Give the gift of life-changing education! Donate Now!
After tossing a drawing pin a large number of times the relative frequency of it landing point up is \(\frac{Number of times with point up}{total number of tosses}\) this can be thought of as the experimental probability.
Sample spaces, events and equally likely outcomes
A sample space is the set of all possible outcomes, all equally likely.
An event is a set of possible outcomes.
P(A) = \(\frac{Number of ways A can happen }{Total number in the sample space}\) = \(\frac{n(A)}{N}\)
where N is number in sample space.
Probability rules and Venn diagrams
All outcomes must be equally likely to happen.
P(A) = \(\frac{N(A)}{N}\)
P(A’ ) =P(A ̅)=P(not A) = 1 – P(A)
P(A∪B)=P(A)+P(B)-P(A∩B)
means the probability that A has occurred given that we know that B has already occurred, and should always be re-written as
P(A|B) = \(\frac{P(A ∩ B}{P(B)}\)
Diagrams for two dice etc.
When considering two dice, two spinners or a coin and a die, the following types of diagram are often useful – they ensure that all outcomes are equally likely to happen.
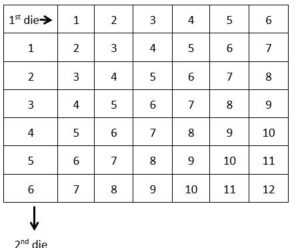
Two dice
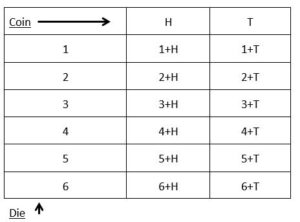
Coin and die
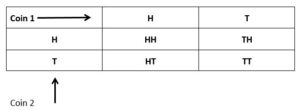
Two coins
Three Coins :
HHH, HHT, HTH, THH, HTT, THT, TTH, TTT
From these diagrams, in which all outcomes are equally likely, it should be easy to see that
For two dice: P ( total 10 ) = \(\frac{3}{36}\)
P ( total 10| 4 on 1st die ) = \(\frac{P (total 10 ∩ 4 on 1st die)}{P(4 on 1st die)}\) = \(\frac{\frac{1}{36}}{\frac{6}{36}}\) = \(\frac{1}{6}\)
For coin and die:
P(Head and an even number) = \(\frac{3}{12}\)
For three dice:
P(exactly two Heads) = \(\frac{3}{8}\)
Tree diagrams
The rules for tree diagrams are :
Select which branches you need
Multiply along each branch
Add the results of each branch needed.
Make sure that you include enough working to show which branches you are using (method).
Be careful to allow for selection with and without replacement.
Example 1: In the launch of a rocket, the probability of an electrical fault is 0.2. If there is an electrical fault the probability that the rocket crashes is 0.4, and if there is no electrical fault the probability that the rocket crashes is 0.3.
Draw a tree diagram. The rocket takes off, and is seen to crash. What is the probability that there was an electrical fault?
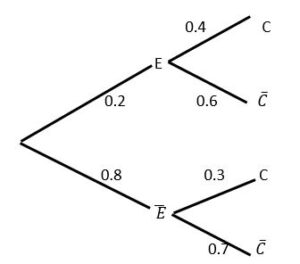
Solution : Let E be an electrical fault and C be a crash
We need !!
Independent events
Definition.
A and B are independent ⇔
It is also true that
A and B are not linked, they have no effect on each other.
Example:
A and B are independent events. and . Find P(B).
Answer :
⇒
But since A and B are independent
⇒
⇒
Exclusive events
Definition.
A and B are mutually exclusive ⇔ P(A ∩ B) = 0
i.e. they cannot both occur at the same time
⇒ P(A ∪ B) = P(A) + P(B)
Example:
Prove that A and B are mutually exclusive.
Answer :
⇒
⇒
⇒ P(A ∩ B) = 0
⇒ A and B are mutually exclusive.
Number of arrangements
Example: A bag contains 5 Red beads, 7 Yellow beads, and 6 White
beads. Three beads are drawn without replacement from the bag. Find the probability that there are 2 Red beads and 1 Yellow bead.
Answer:
These beads can be drawn in any order, RRY, RYR, YRR
⇒