Give the gift of life-changing education! Donate Now!
An interval is a set of (real) numbers between two values. So, for example, ( 0 , 1)is all of the real numbers x such that 0 < x < 1 .
If we have an unknown parameter, we may find an estimator for this parameter and use for the parameter. However, how reliable this estimate is we do not know. This is where confidence intervals come in. Instead of estimating the parameter, we say that there is a 95% (or some other percentage) chance that a given interval contains the parameter.
For example, suppose we have an unknown parameter q. If the probability that the interval (a,b) contains q is 0.95, i.e. if P (a < q < b) = 0.95 then (a , b) is known as the 95% confidence interval for q.
N.B. q is fixed and it is the interval which varies. It is therefore incorrect to say that there is a 95% chance that q lies in the interval. Rather, there is a 95% chance the interval contains q (a subtle, but important difference!).
Constructing Confidence Intervals
If the random variable X has a normal distribution with mean μ and variance σ2, then the sample mean X also has a normal distribution with mean m, but with variance \(\frac{s^2}{n}\) (see random samples). In other words,
X ̅~N(m,\(\frac{s^2}{n}\)) .
In fact, if we have a random variable X which has any distribution (not necessarily normal), by the central limit theorem the distribution of X will be approximately normal with mean m and with variance \(\frac{s^2}{n}\), for large n.
So standardising this, we get:
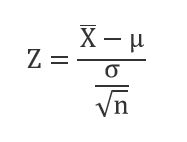
(since the mean is μ and the standard deviation is \(\)\frac{s}{\sqrt{n}} ).
From the Normal Distribution section, we know that P ( - 1.96 < Z < 1.96 ) = 0.95.
P( -1.96 < \(\)\frac{\bar{x} - μ }{σn}[\latex] < 1.96 ) = 0.95
Rearranging this we get
P [X
Hence the 95% confidence interval for m is:
(X