Give the gift of life-changing education! Donate Now!
Radian Measurement of Angles
\(x^2\)
Review Required Skills
Parts of Circle:
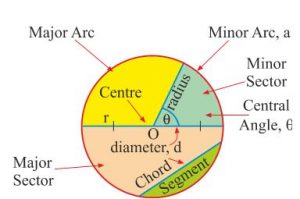
Term
Diameter=d , Circumference = C , Area = A , Angle for full circle = 360°
Formula for Circle of radius, r
Example : Quick Review of Required Skills
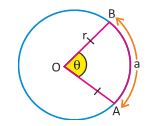
Consider circle with radius r where the minor arc a subtends an angle θ at the center O, as shown in the figure, for the following examples.
Q1. Find circumference for a circle with area of 16π m2
Solution : Calculate radius from given area and the find the circumference.
A=πr2⇒16π=πr2⇒r=4
C=πd=2πr=2π(4)=8π
Circumference of the circle is 8π m.
Q2. Find area of the sector for r=10,θ=60°
Solution : Area of the circle=πr2
Since the sector angle is 60° and full circle angle is 360°, sector area will be one-sixth of that of the circle area.
![]()
Q3. Find length of the arc, a, for r=8 m,θ=120°
Solution : Circumference of a circle=2πr
Since angle subtended by the arc is 120° and full circle angle is 360°, arc length will be one-third of that of the circumference.
![]()
Radian
Radian is the standard unit for measuring angles.
Its symbol is C. Angle measurement of 2 radians can be written as 2 radians, 22, 2 rad or even just the number 2. The word ‘radian’ is an abbreviation of ‘radial’ angle.

In the figure, a is the arc length that subtends and angle θ at the center of a circle with radius r. For a given angle θ, the ratio of arc length to radius is always constant. This ratio represents the angle in radians.
The central angle is one radian when arc length a is equal to the length of the radius r.
For a unit circle the length of an arc is numerically equal to the radian measure of the angle .
Alternate Proof for θ = ![]()
In a circle angle θ subtended is proportional to the arc length
 (1)
(1) 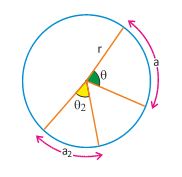
If a2=r then θ2= 1 radian
substituting we get
![]() (2)
(2)
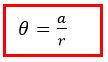

![]()
Example: Subtended angle from radius and arc length
| Question | Solution | |
| a. | Find the measure of central angle that is subtended by an arc length of 10 cm in a circle with radius 4 cm. | 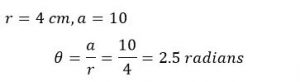 |
| b. | Find the measure of central angle that is subtended by an arc length of 3 cm in a unit circle.
NOTE: Unit circle has radius of 1 |
Angle subtended is numerically equal to the arc length
|
Example : Subtended angle from radius and arc length
| Question | Solution | |
| a. | Find arc length of a circle with radius of 10 cm if central angle is 2c. |
|
| b. | Find the radius of the circle where arc length of 6 cm subtends an angle of 2 radians at the center. | 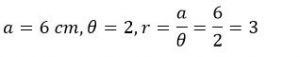 |
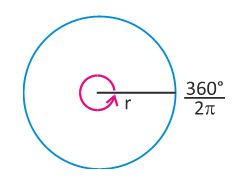
Example 4: Angle subtended by a full circle
Show that the angle subtended by one rotation is
Solution 4: Angle subtended by a full circle
 |
 |
Example 5: Find arc length for given angle in a unit circle
Major arc on a unit circle subtends an angle of 5π/3 . Find exact length of the arc.
Solution 5: Find arc length for given angle in a unit circle
| Unit circle has radius, r =1
Angle subtended, θ= 5π/3
θ= r/a NOTE: For unit circle arc length is equal to angle in radians
|
Radian – Degree Conversion
One full revolution of a point on the circle will subtend and angle of 360° or 2π radians.
These angles are equal. Therefore, 360°=2π radians ⇒180°=π radians


Example 1 : Degree – Radian Relation
| Question | Answer | |
| a. | Find measure if 1 degree in radians | $$ 1 degree=\frac{π}{180°} radians= 0.017453 radians$$ |
| b. | Find the measure of 1 radian in degree | $$1 radians=\frac{π}{180°} = 57.297°=57.3°$$ |
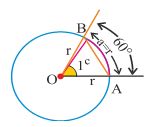 NOTE: Equilateral triangle of side length r, as shown in the figure illustration that 1c is slightly less than 60°. NOTE: Equilateral triangle of side length r, as shown in the figure illustration that 1c is slightly less than 60°. |
||
| Example 6: Convert Degrees to Radians
Convert angles in degrees to radians in exact form
|
Example 7: Convert Radians to Degrees
Convert following angles in degrees to radians
|
||||||||||||||
| Solution 6 | Solution 7 | ||||||||||||||
| a. | $$120°=120°×\frac{π}{180°}=\frac{2}{3}π$$ | a. | $$2.5^c=2.5^c×\frac{180}{π}=143.2394≈143.24°$$ | ||||||||||||
| b. | $$225°=225°×\frac{π}{180°}=\frac{5}{4} π$$ | b. | $$0.4π=0.4π×\frac{180}{π}=72°$$ | ||||||||||||
| c. | $$400°=400°×\frac{π}{180°}=\frac{20}{9} π$$ | c. | $$\frac{π}{15}=\frac{π}{15}×\frac{180}{π}=12°$$ | ||||||||||||

Table 1: Degree and radian measures of some common angles
| Degrees | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
| Radians | 0 | $$\frac{π}{6}$$ | $$\frac{π}{4}$$ | $$\frac{π}{3}$$ | $$\frac{π}{2}$$ | $$\frac2{π}{3}$$ | $$\frac{3π}{4}$$ | $$\frac{5π}{6}$$ | π |
| Degrees | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° | |
| Radians | $$\frac{7π}{6}$$ | $$\frac{5π}{4}$$ | $$\frac{4π}{3}$$ | $$\frac{3π}{2}$$ | $$\frac{5π}{2}$$ | $$\frac{7π}{2}$$ | $$\frac{11π}{2}$$ | 2π | |
Practice Q1: Convert from degrees to radians. Write exact and decimal equivalent.
a. 30°
b.135°
c.-90°
d.200°
e.-250°
Answers Q1
$$a. 30°=\frac{π}{6}=0.5236^c$$
$$b. 135°=\frac{3π}{4}=2.3562^c$$
$$c. -90°= \frac{-π}{2}=-1.5708^c$$
$$d. 200°=\frac{10}{9} rad=3.4906^c$$
$$r. -250°=\frac{-25π}{18}=4.3633^3$$
Note: When writing radian measure as fractional multiple of unit c is normally not required. Radian measure in terms of is more meaningful and is preferred over its decimal equivalent.
Practice Q2 : Convert each angle in radian to degrees. Show all the steps. Round to 2 decimal places, if required.
$$\frac{π}{3} radian$$
$$\frac{3π}{2} radian$$
$$\frac{-5π}{6} radian$$
$$3 radians$$
Answers Q2
$$\frac{π}{3} radian=60°$$
$$\frac{3π}{2} radian\270°$$
$$\frac{-5π}{6} radian=-150°$$
$$3 radians=171.89°$$
Note: Unit of radians is normally dropped when angle measure is given in faction of π.
Solution to Student’s Activity 1
Table 1: Convert the rotations around a circle into angles in radians and degrees.
| The table below to write angle subtended at the centre by the given revolution | ||
| Part
Revolution |
Angle subtended in Radians | Angle subtended in Degrees |
| $${1 revolution}$$ | $${2π}$$ | $${360°}$$ |
| $$\frac{1}{2}revolution$$ | $$\frac{1}{2} ×{2π}={π}$$ | $$\frac{1}{2} ×{360°}={180°}$$ |
| $$\frac{1}{4}revolution$$ | $$\frac{1}{4}×\frac{ 2π}{2}=\frac{ π}{2}$$ | $$\frac{1}{4} ×{360°}={90°}$$ |
| $$\frac{3}{4}revolution$$ | $$\frac{3}{4}×{ 2π}=\frac{ 3}{ 2π}$$ | $$\frac{3}{4} ×{360°}={270°}$$ |
| $$\frac{1}{8}revolution$$ | $$\frac{1}{8}×{ 2π}=\frac{ π}{4}$$ | $$\frac{1}{8} ×{360°}={45°}$$ |
| $$\frac{1}{8}revolution$$ | $$\frac{1}{6}×{ 2π}=\frac{ π}{3}$$ | $$\frac{1}{6} ×{360°}={60°}$$ |
| $$\frac{1}{12}revolution$$ | $$\frac{1}{12}×{ 2π}=\frac{ π}{6}$$ | $$\frac{1}{12} ×{360°}={30°}$$ |
| $${0 revolution}$$ | $${0}×{ 2π}={0}$$ | $${0}×{360°}={0°}$$ |
| $$\frac{5}{6}revolution$$ | $$\frac{5}{6}×{ 2π}=\frac{ 5π}{3}$$ | $$\frac{5}{6} ×{360°}={300°}$$ |
| More than one revolution | ||
| $${2 revolution}$$ | $${2}×{2π=4π}$$ | $${2}×{360°}={720°}$$ |
| $$3\frac{1}{2}revolution$$ | $$3\frac{1}{2}+{2π}={7π}$$ | $$3\frac{1}{2}×{360°}={300°}$$ |
| Degree and radian relation for some angles.
|
Sketch Angles with Radian Measurement
Protractors are in degrees. So, how do we draw angles given in radians?
We observed from the Table 1 that the angles in radians can be represented as factions of a revolution. One full revolution represents angle of 2π radians and half of the revolution is π radians. To draw any angle in radians we need to divide the circle in the required denomination as illustrated in the examples.
\begin{document}
\hspace*{-3cm}
$$ {Example 8: Steps to Sketch Angle of } \frac{4π}{3} $$
\end{document}
$${To sketch an angle of }\frac{4π}{3}{we need 4 angles of}\frac{π}{3}$$
$${πrepresent the angle of semi-circle (a straight line).} \ { Divide semi-circle in three equal parts (or circle in 6 equal parts) to get angle of }\frac{π}{3}\ { each.}\frac{4π}{3} \{ is the fourth} \frac{π}{3}{as shown in the figure.}$$
Convert Decimal to Degree(DMS), Minute, Seconds Form
1 degree =60 minutes
1 minute =60 seconds
1 degree =3600 seconds