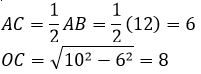Give the gift of life-changing education! Donate Now!
Area: Composite Shape
Q1 ∆ABD and ∆BCD are right angle triangles as shown in the figure. AB is parallel to CD
Find area of the triangle ∆ABC
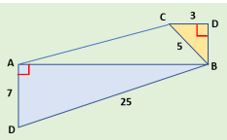
Solution
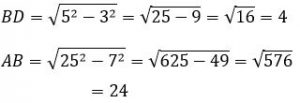
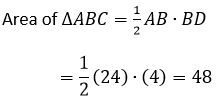
Q2 : Application
Find area of the shaded region, DEB, in the rectangle ABCD as shown in the diagram.
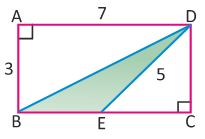
Triangle DCE is a right triangle with DE as the hypotenuse and DC = 3
Find EC using Pythagorean Theorem.
Area of shaded region is area of rectangle – (Area of )
Solution
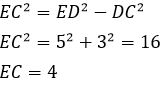

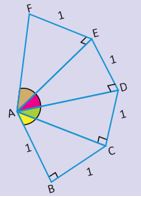
Q 3: Application
The figure shows four right triangles with common vertex at and a side of unit length.
∆ABC is a right isosceles triangle with legs of unit length.
 Solution
Solution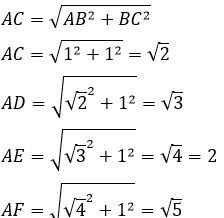
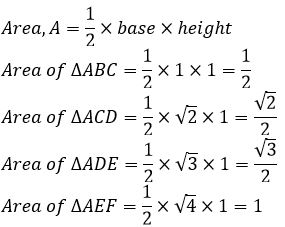 The length of each hypotenuse is √n, n=2,3,4,5Note: This is how the ancient Greeks constructed accurate length of √n.
The length of each hypotenuse is √n, n=2,3,4,5Note: This is how the ancient Greeks constructed accurate length of √n.Q4: Height of Pyramid
The great Pyramid at Giza in Egypt has a square base with sides 220 m long. The distance from the top of the pyramid to each corner of the base is 233 m. Find the height of the pyramid.

Solution : Height of Pyramid
ABCD, the base of the pyramid is a square. Triangle ABC is right triangle.
Solve ∆ACB to find diagonal. Half of this diagonal helps to find the height while solving the ∆AOE.


Answer: Height of the pyramid is 173.5 m.
Q5. Find the longest diagonal length, AD, in the rectangular prism with dimensions of 3, 4, and 8 units. Round answer to 3 s.f.
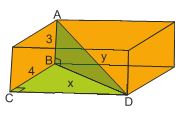
Solution :
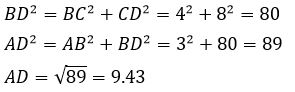
Q6. Find the height of the square based prism shown in the figure correct to 3 significant places.
Solution :
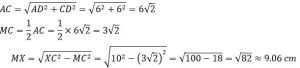
Q7. A wedge with square base is shown in the figure.
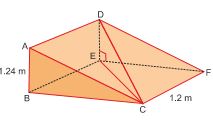
Find the length DC if the sides of the square are 1.2 m each and the height AB is 1.24 m.
Solution :
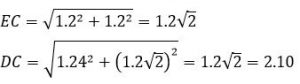
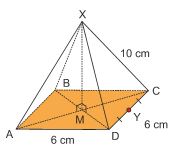
Q8. Find the distance of the chord AB from the center O of the circle with radius 10 cm if the chord length is 12 cm.

Solution :
Let OC be right bisector of AB
∆OCA is a right triangle since the right bisector of a chord will pass through the origin.