Give the gift of life-changing education! Donate Now!
9.1 Moments in Statics
The moment of a force is
Moment = Force x r (positive is anticlockwise)
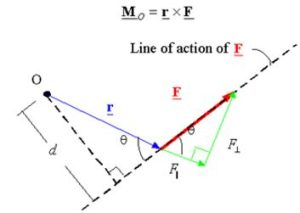
The moment of \(\vec{F}\) about the point O is M=\(\vec{F}\) * d = F* rsinθ
The resultant moment is the difference between the sum of the anticlockwise moments and the sum of the clockwise moments.
Uniform Lamina : Usually Rectangular of uniform density, the center of mass is the center of the rectangle.
For uniform triangular lamina, the center of mass is the centroid of the triangle.
Uniform rod : The center of mass is at the mid-point of the rod
Equilibrium : If an object is in equilibrium, the resultant force is zero and the sum of the moments is zero.
\(\sum{\vec{F}}\) = \(\vec{0}\)
\(\sum{M}\) = \({0}\)
To solve problems :
– Draw a diagram showing all the forces
– Take moments about any point O. The moment of the Force passing through O is zero
– Resolve the forces along the x-axis and along the y-axis
Types of problems in statics :
Ladder against a wall
– Inclined plane
– A door
– An object in equilibrium held by 2 strings of unequal length