Give the gift of life-changing education! Donate Now!
– Equation of the straight line
The equation of a straight line is
y=mx+b where m is the gradient and b is the y-intercept.
The equation of a tangent to a curve is
y – f(x0) = f'(x0)(x – x0)
f'(x0) is the slope of the line at the point x0 and passes through the point (x0 , f'(x0))
If the slope of 2 lines are m=m’, the lines are parallel
If the slope of 2 lines are m= – \(\frac{1}{m'}\) , the lines are perpendicular
– The circle
The equation of the circle with center (h,k) and radius r is
(x – h)2 + (y – k) 2= r2
The general equation of the circle is
x2 + y2 + 2gx + 2fy + c = 0
The center of the circle and the radius can be obtained by completing the square.
The angle in a semicircle is a right angle.
The perpendicular from the center of a circle to a chord bisects the chord.
The radius of a circle is perpendicular to the tangent at its point of intersection.
– Parametric Equations
The parametric equations 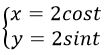 describes a circle center O and radius =2
describes a circle center O and radius =2
The equations ![]() describes a circle center (3,-2) and radius 4
describes a circle center (3,-2) and radius 4
The equations 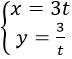 describes the rectangular hyperbola xy = 9
describes the rectangular hyperbola xy = 9
{ y =\(\frac{3}{t}\)
– Modelling with parametric equations
Use of parametric equations in kinematics (Parabolic trajectory)
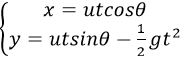
-Conversion of cartesian coordinates to polar coordinates
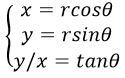 and \(x^2 + y^2\)
and \(x^2 + y^2\)