Give the gift of life-changing education! Donate Now!
5.1 Probability
Probability – is the branch of mathematics of chance and is the study of randomness. lt tends to be used to predict events and is the measure of the likelihood that an event will occur.
– is quantified as a number between 0 and L, where, C indicates impossibility and 1 indicates certainty.
For instance,
How likely is it going to snow tomorrow?
What are the chances that you will get an 90% in this course?
What are the odds that the TTC will go on strike?
ln this unit we will attempt to learn mathematical concepts in probability to help us understand and predict events that might happen.
Types of Probability
1. Empirical Probability – based on direct observation or experiment.
2. Theoretical Probability- based on mathematical analysis.
3. Subjective Probability – based on informed guesswork, intuition, previous experience.
Key Terms
Sample Space – the set of all possible outcomes in a probability experiment.
Trial– a step in a probability experiment in which an outcome is produced and tallied.
Event – a subset of a sample space.
Outcome – A possible result, a component of an event.
Example : Determine the possible outcomes of each trial and n(s) for each experiment.
a) Tossing a coin.
S = { Heads , Tail } n(s) = 2
b) Tossing two coins
S = {HH , HT , TH , TT , } n(s) = 4
c) Rolling a die.
S = {1 , 2 , 3, 4 , 5 , 6 } n(s) = 6
ln this course, we are primarily concerned with theoretical probability.
The probability of an event A is given by:
P(A) = \(\frac{Number of Favorable Out Comes To A}{Total Out Come }\)
Or P(A) = \(\frac{n(A)}{n(S) }\) , 0 ≤ P(A) ≤ 1
where P(A) = probability of event A
n(A) = number of outcomes of A
n(S) = total number of outcomes of sample space
The sum of all probability of all possible events is always equal to 1:
1 = P(A) + P(A’) : probability of an event not occurring
P(A’) = 1- P(A)
P(A)= 1- P(A’)
Note: Sometimes finding the numerator or denominator requires a Permutation or a Combination
Many probability questions involve playing cards and dice. The images below can be helpful.
Cards

1. 12 Face cards (4J, 4Q, 4K)
2. 26 black,26 red cards
Rolling 2 Dice
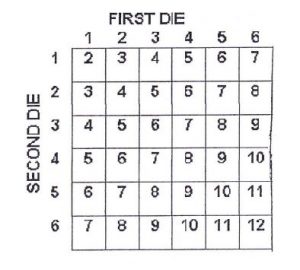
n(S)= 36 ways
Complementary Event
The complement of A, denoted by A’ , consists of all the outcomes in which the event A does not occur.
P(A)+P(A’): 1
P(A) :1- P(A’)
Depending on the problem, it may be easier to find P(A’) and then use the above equation to find P(A).
5.2-PROPERTIES USTNG COUNTTNG TECHNTQUES
ln the previous lesson, we learned that the classical approach to assigning probability to an event involves determining the number of elements in the event and the sample space. There are many situations in which it would be too difficult and too tedious to list all of the possible outcomes in a sample space. ln this lesson, we will learn various ways of counting the number of elements in a sample space without actually having to identify the specific outcomes. The specific counting techniques we will explore include the multiptication rule, permutations and combinations.
EXAMPLE 1: A soccer player takes three penalty kicks. The outcome is noted as a Goal (G) or a Miss (M).(Assume the goal to miss ratio is the same).
a) Draw a tree diagram to illustrate the experiment.
b) Determine the probability of exactly 3 goals.
c) Determine the probability that there are more goals than misses.
Probability using Permutations
Number of permutations (order matters) of n things taken r at a time:
P(A) = \(\frac{n!}{(n-r)! }\)
Probability using Combinations
Number of combinations (order does not matter) of n things taken r at a time:
C(n , r) = \(\frac{n!}{(n-r)!r! }\)
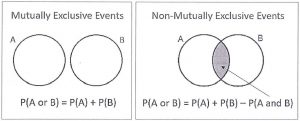
5.3 – MUTUALLY EXCLUSIVE EVENTS
Mutually Exclusive are events that cannot happen at the same time. There is no overlap when two or more events are occurring. These are also called disjoint events. lf A and B are mutually exclusive events, then the probability of either A or B occurring is:
P(A or B) = P(A ∪ B) = P(A) + P(B)
Non- Mutually Exclusive Events are events that can occur simultaneously (there is some overlap).
lf A and B are non- mutually exclusive events, then the probability of either A or B occurring is:
P(A or B) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
5.4 – INDEPENDENT EVENTS
What is an independent event?
Independent events are events where the outcome of one event does not affect the outcome one event does not affect the out come of the other events.
Example: Tossing a coin and rolling a number cube are independent events.

lf two events, A and B are independent events (do not influence one another), then the probability that both A and B happens is:
P(A and B) = P(A ∪ B) = P(A) x P(B)
5.5 – DEPENDENT EVENTS & CONDTTTONAL PROBABTLTTY


lf B is dependent on event A, then the conditional probability of A and B occurring is:
P(A ∩ B) = P(A) x P(A | B)
Independent Events
The outcome of one event does not affect the outcome of the other. lf A and B are independent events then the probability of both occurring is:
P(A and B) -P(A) x P(B)
Dependent Events
The outcome of one event affects the outcome of the other. lf A and B are dependent events then the probability of both occurring is
P(A and B) -P(A) x P(B | A)