Give the gift of life-changing education! Donate Now!
19.2- Pythagoras’ theorem
Know the formulae for: Pythagoras’ theorem a2+ b2=c2 , and the
trigonometric ratios,
\({sin θ}\) = \(\frac{opposite}{hypotenuse}\)
\({cos θ}\) = \(\frac{adjacent}{hypotenuse}\)
\({tan θ}\) = \(\frac{ opposite}{adjacent}\)
Apply them to find angles and lengths in right-angled triangles in two-dimensional figures
19.3-Trigonometry 1
• Interpret and use three-figure bearings
• apply Pythagoras’ theorem and the sine, cosine and tangent ratios for
acute angles to the calculation of a side or of an angle of a right-angled
triangle
• solve trigonometrical problems in two dimensions involving angles of
elevation and depression
• extend sine and cosine functions to angles between 90° and 180°
• solve problems using the sine and cosine rules for any triangle and the
formula area of triangle = \(\frac{1}{2}abc sin c\)
• solve simple trigonometrical problems in three dimensions
19.4-Trigonometry 2
Measured clockwise from the north, i.e. 000°–360°.
e.g. Find the bearing of A from B if the bearing of B from A is 125°
Angles will be quoted in, and answers required in, degrees and decimals of a degree to one decimal place.
Calculations of the angle between two planes or of the angle between
a straight line and plane will not be required.
19.5-Pythagoras and Trigonometry problem
Know the exact values of sin θ and cos θ for θ = 0°, 30°, 45°, 60° and 90°;
know the exact value of tan θ for θ = 0°, 30°, 45° , 60° and 90°
19.6- Vectors
• Describe a translation by using a vector represented by
\(\dbinom{x}{y}\), \(\vec{AB}\) or a
• add and subtract vectors
• multiply a vector by a scalar
• calculate the magnitude of a vector\(\dbinom{x}{y}\) as \(\sqrt{x^2 + y^2}{y}\)
• represent vectors by directed line segments
• use the sum and difference of two vectors to express given vectors in
terms of two coplanar vectors
• use position vectors
19.7 – Summary and Review
Question1 : If \(\vec{a}\) = \(\dbinom{6}{-10}\) , \(\vec{b}\) = \(\dbinom{-1}{2}\) and \(\vec{c}\) = \(\dbinom{-4}{7}\)
Calculate \(\vec{a} + \vec{b} + \vec{c}\) and Show that \(\vec{a} + 2\vec{c}\) = \(k\vec{b}\) where k is an integer ?
19.8- Assessment 19
Question 1 : Use trigonometry to work out the length x ?

Question 2 : The vector \(\dbinom{3}{2}\) translates A to B. Calculate the vector that translates B to A ?
Question 3 : Given the triangle ABC such that AB=15 cm, \(\cap{A}\) =34°, \(\cap{B}\) =42°, \(\cap{C}\) =104°, Calculate AC ?
Question 4 : Solve the following equations :
cosx= cos 60° ( for 90°≤x≤306°)
cosx=- cos 60° ( for 180°≤x≤360°)
Question 5 : Lisa and Tila are walking towards a shop along different straight paths.
The diagram shows their positions at 2 pm
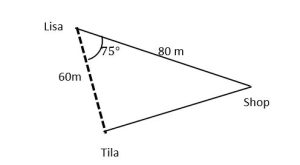
Assume they walk at the same speed. Who will arrive at the shop first?