20.1- Introduction
Question 1 : A coin is flipped 4 times, Calculate the probability of getting 4 Heads?
20.2- Sets
Use language, notation and Venn diagrams to describe sets and
represent relationships between sets
Definition of sets:
e.g.
A = {x∶ x is a natural number}
B = {(x,y): y = mx + c}
C = {x∶ a ≤ x ≤ b}
D = {a,b,c…}

Includes using Venn diagrams to solve problems.
Notation:
Number of elements in set A n(A)
“… is an element of …” ∈
“… is not an element of …” ∉
Complement of set A A’
The empty set ∅
Universal set ξ
A is a subset of B A ⊆ B
A is a proper subset of B A ⊂ B
A is not a subset of B A ⊈ B
A is not a proper subset of B A ⊄ B
Union of A and B A ∪ B
Intersection of A and B A ∩ B

20.3-Probability Spaces
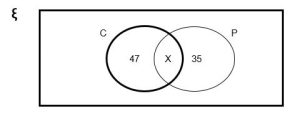
Question 1 : Here are some information about 150 students.
ξ = 150 students
C = students who study Chemistry (47+x)
P = students who study Physics (35 +x)
X = students who study both physics and Chemistry
The probability that a Physics student, chosen at random, also studies Chemistry is \(\frac{5}{12}\) . One of the 150 students is chosen at random.
Calculate the probability that the student does not study either Chemistry or Physics ?

20.4-Tree diagrams
Question 1 : Two ordinary fair dice are rolled. Complete the tree diagram?

20.5- Conditional Probability
Question 1 : A coin is thrown followed by a dice. What’s the probability of getting a Head followed by a 3? If you get a 3, What’s the probability that the coin was a Head?

20.6- Summary and Review
Question 1 : The probability that A is the outcome of an experiment is 0.2 . Calculate the probability that A is not the outcome?

20.7 Assessment 20
Question 1 : A coin is thrown 50 times. It lands on heads 31 times.
(a) Calculate the relative frequency it lands on heads?
Question 2 : A biased dice is thrown. Here are the probabilities of each.

Score

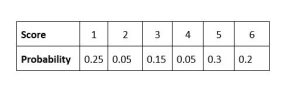
The dice is thrown 200 times.
Calculate the expected number of times the score will be odd?

20.8- Lifeskills 3 : Getting ready
Question 1 : There are only r red counters and g green counters in a bag. A counter is taken at random from the bag. The probability that the counter is green is\(\frac{3}{7}\) The counter is put back in the bag. 2 more red counters and 3 more green counters are put in the bag. A counter is taken at random from the bag. The probability that the counter is green is \(\frac{6}{13}\) Find the number of red counters and the number of green counters that were in the bag originally?