22.1- Introduction
• use current units of mass, length, area, volume and capacity in
practical situations and express quantities in terms of larger or
smaller units
Convert between units including units of area and volume.
e.g. between mm2 and cm2 or between cm3 , m3 and litres

22.2-Compound units
Change freely between related standard units (e.g. time, length, area, volume/capacity, mass) and compound units (e.g. speed, rates of pay,
prices, density, pressure) in numerical and algebraic contexts
A Compound measurement is a measurement that uses more than one quantity.
Density
Density is calculated by mass ÷ volume. So density is therefore written as mass per volume.
The most common units used to measure density are\(\frac{kg}{m^3}\) kilograms divided by metres cubed, or \(\frac{g}{cm^{-3}}\) or g cm^-3grams divided by centimetres cubed.
Speed
Speed is measured using the formula distance ÷ time. So this will therefore be written as distance per time.
The most common units used to measure speed are mph (miles per hour) or km/h (kilometres per hour)
Question 1 : A car travels 3.5 miles in 5 minutes. Calculate the average speed in miles per hour?

Rates of Pay
Rates of pay are given for a unit of time for example £20/h (twenty pounds per hour) or £750/week or £3,250/month or £39,000/annum.
Question 2 : Katy invests £200 000 in a savings account for 4 years. The account pays compound interest at a rate of 1.5 % per annum. Calculate the total amount of interest Katy will get at the end of 4 years ?

22.3-Converting between units
Question 1 : In this question, use 1 foot = 12 inches
1 inch = 2.5 centimetres
Change 5 feet 8 inches to centimetres ?
Question 2 : How many minutes are there in 5 \(\frac{1}{4}\) hours?

22.4-Direct and Inverse proportions
Solve problems involving direct and inverse proportion, including graphical and algebraic representations
Question 1 : h is inversely proportional to p and p is directly proportional to \(\sqrt{t}\) ; Given that h = 10 and t = 144 when p = 6: Find a formula for h in terms of t?

22.5-Rates of change
Question 1 : Volume of a sphere=\(\frac{4}{3}πr^3\) where r is the radius. A container is a hemisphere of radius 30 cm. Sand fills the container at a rate of 4000 cm3 per minute.Will it take less than a quarter of an hour to fill the container?

22.6- Growth and decay
Compound growth and decay are an extension on percentages and are used to model real world applications such as interest, disease and population.
Compound Growth and Decay Formula
The following formula for compound growth and decay enables you to substitute in values to calculate the growth or decay. Knowing and understanding this formula is essential.
\({N}\)= \(N_0 × (1 ± \frac{percentage}{100})^n\)
N= Amount after a period of time
\({N_0}\) = The original amount
Number of periods = n (days, hours, minutes,…)
+ = growth and – = decay
Question 1 : Question 1: Sun wins the lottery and chooses to deposit $ 1,400,000 into a savings account which offers annual compound interest. How much money will she have in this account after 44 years?

22.7- Summary and Review
Question 1 : Given that x2 : (3x + 5) = 1 : 2 find the possible values of x ?

22.8-Assessment 22

Question 1 : A sunflower is 1.8 m tall. Over the next month, it grows a further 34 cm. How tall is the sunflower at the end of the month?

Question 2 : Peter is a long distance runner. In a training session he runs around the 400 m track 23 times. He wanted to run a distance of 10 km. How many more times does he need to run around the track to achieve this?

Question 3 : A water cooler comes with water containers that hold 12 l of water. The cups provided for use hold 150 ml. A company estimates that each of its 20 employees will drink 2 cups of water a day. How many 12 l bottles will be needed for each working week (Monday to Friday)?

Question 4 : David is a farmer and has 52 goats. He is given a bottle of wormer that contains 0.3 litres. The bottle comes with the instructions:
‘Use 4 ml of wormer for each 15 kg of body weight.’
The average weight of David’s goats is 21 kg and he wants to treat all of them. Does David have enough wormer?

Question 5 : The coordinates of triangle ABC are A=(8,1),B= (6,-1), and C=7,-1). Enlarge triangle ABC by scale factor –2, centre (4, 1) ?

22.9- Revision exercise 3
Question 1 : Solve 5(x + 3) < 60 ?
Question 2 : A shopkeeper compares the income from sales of a laptop in March and April

By what fraction does the income from these sales decrease in April?
Question 3 : Solve the equation x²+3x-5=0 ?
Question 4 : Solve the equation 9(x+3)²=4 ?
Question 5 : The graph of y = x² – 1 is reflected in the x-axis to give graph A. Find the equation of graph A ?
Question 6 : The numbers 1 to 12 are put in a grid.
2, 4, 5, 7, 10 and 12 are shown.

Each of the four sides of the grid must add up to 26
Complete the grid using the numbers 1, 3, 6, 8, 9 and 11 ?
Question 7 : Nick has a 6-digit code. He remembers it as three 2-digit numbers. The first number is between 10 and 20 The second number is 3 times the first number. The third number is 5 times the first number.
All six digits are different.
Calculate the code?
Question 8 : BCD is a straight line. Triangle ABC is equilateral. CE = DE

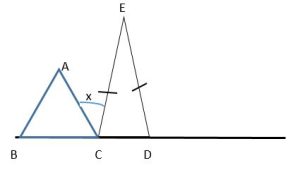
Calculate the angle x ?

Question 9 : Four positive whole numbers add up to 36.
One of the numbers is a multiple of 7 . The other three numbers are equal.
Determine the result when the four numbers are multiplied ?

21.10- Formulae
If r is the radius of the sphere or cone,
l is the slant height of a cone
and h is the perpendicular height of a cone:
Curved surface area of a cone = πrl
Surface area of a sphere = 4πr²
Volume of a sphere = \(\frac{4}{3}πr^3\)
Volume of a cone =\(\frac{1}{3}πr^2h\)