Give the gift of life-changing education! Donate Now!
Q1. (June 2019)
At time t = 0, a parachutist falls vertically from rest from a helicopter which is hovering at a height of 550 m above horizontal ground.
The parachutist, who is modelled as a particle, falls for 3 seconds before her parachute opens.
While she is falling, and before her parachute opens, she is modelled as falling freely under gravity.
The acceleration due to gravity is modelled as being 10 ms-2
(a) Using this model, find the speed of the parachutist at the instant her parachute opens.
When her parachute is open, the parachutist continues to fall vertically. Immediately after her parachute opens, she decelerates at 12 ms-2 for 2 seconds before reaching a constant speed and she reaches the ground with this speed. The total time taken by the parachutist to fall the 550 m from the helicopter to the ground is T seconds.
(b) Sketch a speed-time graph for the motion of the parachutist for 0 ≤ t ≤ T.
(c) Find, to the nearest whole number, the value of T.
In a refinement of the model of the motion of the parachutist, the effect of air resistance is included before her parachute opens and this refined model is now used to find a new value of T.
(d) How would this new value of T compare with the value found, using the initial model, in part (c)?
(e) Suggest one further refinement to the model, apart from air resistance, to make the model more realistic.
Answer :
Initial velocity ,u=0 ms-1
Acceleration, g=10ms-2
Time =3 s
Taking the downward direction as positive
v=u+at
v=u+gt
v=0+10×3=30ms-1
Graph of Speed-time
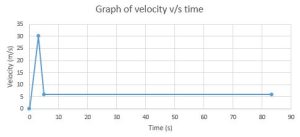
Deceleration, a=-12 ms-2
Time= 2 s
u= 30ms-1
v=30-12 x2=6 ms-1
Distance travelled in
(i)\({s_1}\) = \(ut + \frac{1}{2}gt^2\) = \(0 + \frac{1}{2}* 10 * 9\) = \({45 m}\)
(ii)\({s_2}\) = \(30 * 2 - \frac{1}{2}* 12 * 4\) = 36
(iii)\({s_3}\) = 550 – 45 -36 = 469 m
Time to travel 469 m =(T-5) s
6(T-5)=550-45-36
6T=499
T=83 s
If there is air resistance, T would be greater
Wind , Horizontal motion of the parachute, Buoyancy due to the air.
Q2. (June 2019)
A small ball, P, of mass 0.8 kg, is held at rest on a smooth horizontal table and is attached to one end of a thin rope. The rope passes over a pulley that is fixed at the edge of the table. The other end of the rope is attached to another small ball, Q, of mass 0.6 kg, that hangs freely below the pulley. Ball P is released from rest, with the rope taut, with P at a distance of 1.5 m from the pulley and with Q at a height of 0.4 m above the horizontal floor, as shown in Figure 1. Ball Q descends, hits the floor and does not rebound. The balls are modelled as particles, the rope as a light and inextensible string and the pulley as small and smooth.
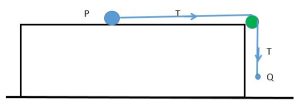
Using this model, (a) show that the acceleration of Q, as it falls, is 4.2 ms-2
(b) find the time taken by P to hit the pulley from the instant when P is released.
(c) State one limitation of the model that will affect the accuracy of your answer to part (a).
Answer :
Let T = tension in the string
0.6g-T=0.6a…………………(1)
T=0.8a…………………………(2)
1.4a=0.6g
a=4.2 ms-2
Time for Q to hit the floor= t_1 s
\({s}\) = \(ut_1 + \frac{1}{2}at_1^2\)
\({4}\) = \(0 + \frac{1}{2}*4.2* t_1^2\)
Time for P to hit the pulley =t_2 s
v=u+at_2
Velocity of P at the pulley=0+4.2*0.436=1.83 ms-1
\({t_2}\) = \(\frac{1.5 – 0.4}{1.83}\) = \({0.601 s}\)
Total time =t_1+t_2=0.436+0.601=1.04 s
The rope is light and inextensible
The pulley is smooth
Q3. A particle, P, moves along a straight line such that at time t seconds, t≥0, the velocity of P, v ms-2, is modelled as
v = 12 + 4t – t2
Find
(a) the magnitude of the acceleration of P when P is at instantaneous rest,
(b) the distance travelled by P in the interval 0 ≤ t ≤ 3
Answer :
v = 12 + 4t – t-2
a =\(\frac{dv}{dt}\)=4-2t
12+4t-t^2=0
(6-t)(2+t)=0
t=6 or t=-2
Acceleration, a=4-2t=4-12=-8 ms-2
|a|=8 ms-2
Distance travelled
\({s}\) = \(\int_0^{3}(12 +4t – t^2\)
= \(|12t + 2t^2 - \frac{1}{3}t^3|_0^{3}\)
Q4. (June 2018)

A plank, AB, of mass M and length 2a, rests with its end A against a rough vertical wall. The plank is held in a horizontal position by a rope. One end of the rope is attached to the plank at B and the other end is attached to the wall at the point C, which is vertically above A. A small block of mass 3M is placed on the plank at the point P, where AP = x. The plank is in equilibrium in a vertical plane which is perpendicular to the wall. The angle between the rope and the plank is α, where tanα = \(\frac{3}{4}\), as shown in the figure . The plank is modelled as a uniform rod, the block is modelled as a particle and the rope is modelled as a light inextensible string.
Using the model, show that the tension in the rope is\(\frac{5Mg(3x+a)}{6a}\), The magntude of the horizontal component of the force exerted on the plank at A by the wall is 2 Mg.
Find x in terms of a.
The force exerted on the plank at A by the wall acts in a direction which makes an angle β with the horizontal.
Find the value of tanβ
The rope will break if the tension in it exceeds 5Mg.
(d) Explain how this will restrict the possible positions of P. You must justify your answer carefully.
Answer:
Taking moments about A
Let the tension in the rope be T
T2asinα=Mga+3Mgx
T2asin(arctan(3/4))=Mg(3x+a)
T = \(\frac{5Mg(3x+a)}{6a}\)
Resolving horizontally
T2acosα=2Mg
\(\frac{5}{6a}*Mg(3x+a)* \frac{4}{5}\) =\({2Mg}\)
3x+a=3a
3x=2a
\({X}\) = \( \frac{2a}{3}\)
Taking moments about B
Force exerted by the wall on the planck =F
Resolving horizontally
Fcosβ=2Mg……………………..(1)
Resolving vertically
Fsinβ + Tsinα=4Mg
Replace T by T = \(\frac{5MG(3x +a)}{6a}\)
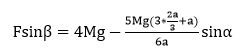
Fsinβ = \(\frac{5MG}{2}\) ……………2
tanβ = \(\frac{\frac{5}{2}}{2}\) = \(\frac{5}{4}\)
(d) \(\frac{5MG(3x + a )}{6a}\) ≤5Mg
(3x+a)≤6a
x ≤ \(\frac{5a}{3}\)
To prevent the rope from breaking, the distance of the block from A must be ≤ \(\frac{5a}{3}\)
Q5.(Edexel Model)
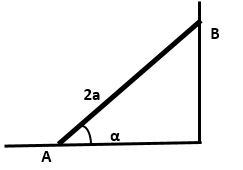
A uniform ladder AB, of length 2a and weight W, has its end A on rough horizontal ground.
The coefficient of friction between the ladder and the ground is 14 .
The end B of the ladder is resting against a smooth vertical wall, as shown above.
A builder of weight 7W stands at the top of the ladder.
To stop the ladder from slipping, the builder’s assistant applies a horizontal force of magnitude P to the ladder at A, towards the wall.
The force acts in a direction which is perpendicular to the wall.
The ladder rests in equilibrium in a vertical plane perpendicular to the wall and makes an angle α with the horizontal ground, where tanα=\(\)\frac{5}{2}\(\)
The builder is modelled as a particle and the ladder is modelled as a uniform rod.
(a) Show that the reaction of the wall on the ladder at B has magnitude 3W.
(b) Find, in terms of W, the range of possible values of P for which the ladder remains in
equilibrium.
Often in practice, the builder’s assistant will simply stand on the bottom of the ladder.
(c) Explain briefly how this helps to stop the ladder from slipping.
Answer :
(a) Reaction of wall on ladder = R
Taking moments about A :
7W*2acosα + Wa cosα=R*2asinα
15Wacosα=2Rasinα
R=\(\)\frac{15w}{2tanα}\(\)=3W
(b) Reaction at A, R1=7W+W=8W
F=μR1=\(\)\frac{1}{4}* 8W\(\)=2W
Pmax=R+F=3W+2W=5W
Pmin=R-F=3W-2W=W
W≤ P≤5W
(c) By standing at the bottom of the ladder, this will increase the reaction R1, thus increasing F which will increase the stability.