Give the gift of life-changing education! Donate Now!
7.1 Position : a vector quantity – distance from a fixed origin
A vector is a quantity which has both magnitude and direction.
Displacement : a vector quantity -measured from the starting quantity (50 m West of starting point)
Distance travelled : a scalar quantity with no direction (125 m)
A scalar is just a number, it has no direction e.g time, mass, length
Average Velocity = \(\frac{Displacement}{Time Taken}\)
Speed = \(\frac{Total Distance}{Total Time}\)
Acceleration = \(\frac{Change of Velocity}{Time}\)
Distance and speed are always positive .
7.2 Graphs in Kinematics
(a) Motion in a straight line

(b) Displacement v/s time
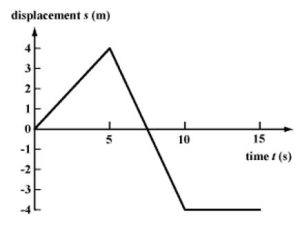
(c) Velocity v/s time
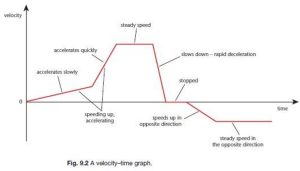
(d) Gradient under the graph
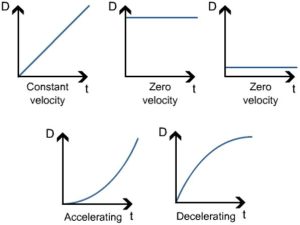
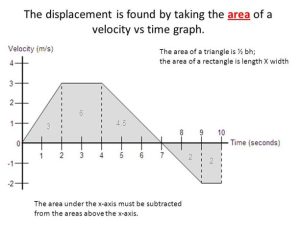
(e) Area under the graph
Example1: A particle is initially travelling at a speed of 2 ms-1and immediately accelerates at for 10 seconds; it then travels at 3ms-2 a constant speed before decelerating at 2 ms-2 a until it stops.
Find the maximum speed and the time spent decelerating.
Sketch a speed-time graph.
If the total distance travelled is 1130 metres, find the time spent travelling at a constant speed.
Solution:
For maximum speed: u = 2, a = 3, t = 10, v = u +at ⇒ c is maximum speed.
For deceleration from 32ms-1 at 2ms-1,the time taken is 32 ÷ 2 = 16 s.
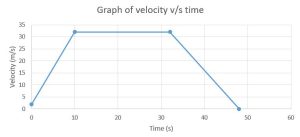
Distance travelled in first 10 secs is area of trapezium = ½(2 + 32) × 10 =170 metres,
distance travelled in last 16 secs is area of triangle = ½ × 16 × 32 = 256 metres,
⇒ distance travelled at constant speed = 1130 – (170 + 256) = 704 metres
⇒ time taken at speed of 32 ms^(-1) is 704 ÷ 32 = 22 s.
7.3 Constant acceleration in a straight line
The equations of motion are :
\({v}\) = \({u + at}\)
\({s}\) = \(ut+\frac{1}{2}at^2\)
\({v^2}\) = \({u^2 + 2as}\)
\({s}\) = \(ut+\frac{1}{2}(u +v)t\)
Example2 : A particle moves through a point O with speed 13ms-1 with acceleration -6 ms-2Find the time(s) at which the particle is 12 m from O.
Solution:
u = 13, a = -6, s = 12, t = ?.
Use s = ut + ½at2 ⇒ 12 = 13t + ½ × (-6) × t^2
⇒ 3t2 – 13t + 12 = 0 ⇒ (3t – 4)(t – 3) = 0
⇒ t = \(ut+\frac{4}{3}at^2\) or 3.
Answer : Particle is 12 m from O after \(ut+\frac{4}{3}at^2\)or 3 s.
Motion in 2D using vectors
Addition of 2 vectors
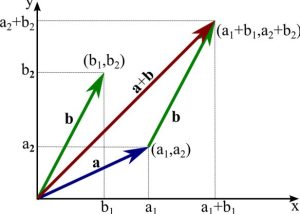
If the vectors are \(\vec{u}\) = \(\dbinom{a}{b}\) and \(\vec{v} +\vec{v}\) = \(\dbinom{a + c}{b + d}\)
\(\vec{r}\) = \({3t}\hat{r} +8t\hat{j}\) (motion in 2D)
7.4 Use of calculus for motion in a straight line
r = f(t) \({v}\) = \(\frac{dr}{dt}\) \({a}\) = \(\frac{dv}{dt}\) = \(\frac{d^2r}{dt^2}\)
\({r}\) = \(\int{vdt}\) \({v}\) = \(\int{adt}\) a = f(t)
Motion in 2D
\(\hat{r}\) = \(t^3\hat{j} + t^{\frac{5}{3}}\hat{j}\)
7.5 Motion under gravity
With vectors

Projectiles
Initial velocity : \(\vec{u}\) = \(\vec{u}cosθ\hat{i} + \vec{u}sinθ\hat{j}\)
Acceleration : \(\vec{a}\) = \(-g\vec{j}\)
Velocity after t s : \(\vec{v}\) = \(\vec{u}cosθ\hat{i} +(\vec{u}sinθ -gt)\hat{j}\)
Particle moving in a horizontal direction reaches maximum height when \(\hat{j}\) = 0 => usinθ – t=0
Displacement after t s
\(\hat{r}\) = \(\vec{u}tcosθ\hat{i} +( \vec{u}sinθ\hat{j}\frac{g}{2}t^2)\hat{j}\)
If the projectile is launched from the ground, it will return to ground when \(\vec{r}\) = 0 => \(\vec{u}tsinθ -\frac{g}{2}t^2\) = 0
Range = total distance travelled in the horizontal direction \({R}\) = \(\frac{u^2sinθ}{g}\)
Example3 : A ball is thrown vertically upwards from O with a speed of 14ms-1
(a) Find the greatest height reached.
(b) Find the total time before the ball returns to O.
(c) Find the velocity after 2 seconds.
Solution: Take upwards as the positive direction.
(a) At the greatest height, h, the velocity will be 0 and so we have
u = 14, v = 0, a = –9.8 and s = h (the greatest height).
Using V2 = u2 + 2as we have 02 –142 = 2 × (–9.8) × h
⇒
h = 196 ÷ 19.6 = 10.
Answer: Greatest height is 10 m.
(b) When the particle returns to O the distance, s, from O is 0 so we have
s = 0, a = –9.8, u = 14 and t = ?.
Using s = ut + ½at2 we have 0 = 14t – ½ × 9.8t2
⇒ t(14 – 4.9t) = 0
⇒ t = 0 (at start) or t = 26/7 s.
Answer: The ball takes 26/7 seconds to return to O.
(c) After 2 seconds, u = 14, a = –9.8, t = 2 and v = ?.
Using v = u + at we have v = 14 – 9.8 × 2
⇒ v = –5.6.
Answer: After 2 seconds the ball is travelling at 5.6 m s-1 downwards.