Give the gift of life-changing education! Donate Now!
8.1 Newton’s First Law and the concept of force
Every object will remain at rest or moves with constant velocity unless an external force is applied
The following are forces .
– W = weight in Newtons (mg=mass(kg) x 9.8ms-2 )
– R = Reaction (normal reactions is at right angles to the point of contact)
– F = Force of friction (acts opposite to the direction at which the object is moving)
-T = Tension in a string
Assumptions :
– Objects are modelled as masses concentrated at a point , no rotational forces
– Strings are inextensible so any stretch can be disregarded (No need to apply Hooke’s Law)
– Strings and rods are light (no mass ) so, their weight can be neglected
– Pulleys are smooth, so no need to consider any frictional force
8.2 Newton’s second Law
The resultant force acting on an object is equal to the acceleration multiplied by its mass
\(\vec{F}\) = \(m\vec{a}\)
8.3 Weight and motion in a straight line under gravity
Value of g is not constant, it varies with the altitude and the geographical location
g = 9.8 ms-2
8.4 Newton’s Third Law
Action and reaction are equal and opposite.
\(\vec{F_{a/b}}\) = – \(\vec{F_{b/a}}\)
Equilibrium of forces
\(\sum\hat{F}\) = \(\hat{0}\)
There is no net force acting on the object
Pulleys and Connected Particles in 2D
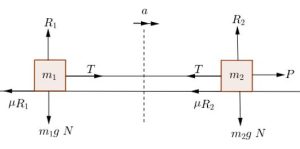 R2 = m2g…………………………………………….(1)
R2 = m2g…………………………………………….(1)
P -T – μR = m2a………………………………….(2)
R1 = m1g……………………………………………..(3)
T – μR1 = m1a……………………………………..(4)
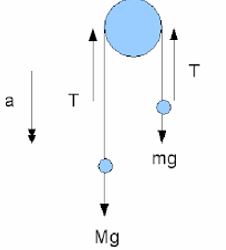
Mg – T = Ma……………………(1)
T – mg = ma…………………….(2)
Equilibrium of a particle under coplanar forces

\(\vec{P} + \vec{Q} + \vec{R}\) = \(\vec{0}\)
8.5 Addition of forces

Example4: F1 and F2 are two forces of magnitudes 9 N and 5 N and the angle between their directions is 100º . Find the resultant force.
Solution: Using the cosine rule
R2 = 52 + 92 – 2 × 5 × 9 × cos 80
⇒ R = 9.50640
and, using the sine rule ,
\(\frac{5}{sinx}\) = \(\frac{9.50640}{sin 80}\) => x = 31.196º
Answer: The resultant force is 9.51 N at an angle of 31.2º with the 9 N force.
Resultant Forces
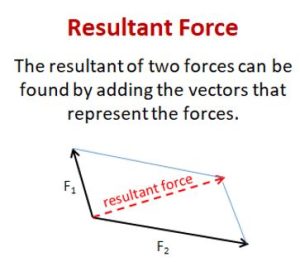
Resultant Force = \(\vec{F_1} + \vec{F_2}\)
Example: Find the resultant of P = 5i – 7j and Q = -2i + 13j.
Solution: R = P + Q = (5i – 7j) + (-2i + 13j) = 3i + 6j.
|R| = \(\sqrt{(3^2 +6^)}\) = \(\sqrt{45N}\)
Answer: Resultant is 3 \(\sqrt{5}N\)
Motion in a plane
8.6 Friction
Coefficient of friction
μ= \(\frac{F}{R}\) F is the force, R is the Normal reaction and μ is the coefficient of friction.
Motion of a body on a rough surface
If a force is acting on the object and the object does not move, then F < μ2R where μd is the coefficient of static friction
When the object is moving, F=μ_d R where μd is the coefficient of dynamic friction.
Limiting Friction
Limiting friction is defined as the friction which is generated between the two static surfaces that come in contact with each other.
Example: A box of mass 30 kg is being pulled along the ground by a horizontal force of 60 N. If the acceleration of the trolley is 1.5 ms-2 , find the magnitude of the friction force.
Solution: No need to resolve as forces are already at 90º to each other.
Resolve horizontally
⇒ 60 – F = 30 × 1.5
=> F = 60 – 45 = 15.
Answer: Frictional force is 15 N.
Statics
The branch of mechanics that deals with bodies at rest or forces in equilibrium.