Quotient Identity

tanθ = \(\frac{sinθ}{cosθ}\)       cotθ= \(\frac{cosθ}{sinθ}\)

Pythagorean Identity
sin² θ + cos2² θ = 1
1 + tan²θ = sec²θ
1 + cot²θ = csc²θ

Rearrange Pythagorean Identity

sin²θ= 1 − cos²θ
sin²θ = (1 + cos )(1 − cosθ )
cos²θ = 1 − sin²θ
cos²θ = (1 + sinθ )(1 − sinθ )

sec²θ − tan²θ = 1
(secθ + tanθ )(secθ − tanθ ) = 1

(secθ + tanθ ) =  \(\frac{1}{(secθ - tanθ)}\)
(secθ – tanθ ) =  \(\frac{1}{(secθ + tanθ)}\)   

csc²θ − cot²θ = 1
(cscθ + cotθ )(cscθ − cotθ ) = 1

(cscθ + cotθ) =  \(\frac{1}{(cscθ - cotθ)}\)   
(cscθ – cotθ) =  \(\frac{1}{(cscθ + cotθ)}\)   

Reciprocal Identity
cscθ = \(\frac{1}{sin}\)  ; secθ = \(\frac{1}{cosθ}\); cotθ =  \(\frac{1}{tanθ}\)

Even Odd Identity
sin(−θ) = −sinθ
cos(−θ) = −cosθ
tan(−θ) = −tanθ
csc(−θ) = −cscθ
sec(−θ) = −secθ
cot(−θ) = −cotθ

Co-Function Identity                                                                       
sin(90° − θ) = cosθ
cos(90° − θ) = sinθ
tan(90° − θ) = cotθ

Related Acute Angle
sin(180° − θ) = sinθ
cos(180° − θ) = −cosθ
tan(180° − θ) = −tanθ
sin(180° + θ) = −sinθ
sin(180° + θ) = −cosθ
sin(180° + θ) = tanθ
sin(360° − θ) = −sinθ
sin(360° − θ) = cosθ
sin(360° − θ) = −tanθ

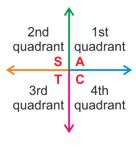
Coordinate Plane Point                       \(S^o_H\) \(C^A_H\) \(T^o_A\)

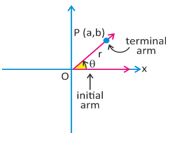
P(a, b ), = \(\sqrt{a^2 +b^2}\) > 0

sinθ = \(\frac{b}{r}\) 
cosθ = \(\frac{a}{r}\)

tanθ = \(\frac{b}{a}\)    ;     cscθ = \(\frac{r}{b}\)    ;  sec θ= \(\frac{r}{a}\)  ;  cotθ = \(\frac{a}{b}\)