Give the gift of life-changing education! Donate Now!
1.1- Introduction
-Identify and use natural numbers , integers (positive,negative and zero) , prime numbers, square numbers, cube numbers, common factors and common multiples, rational and irrational numbers (e.g. π, \(\sqrt{2}\) ), real numbers
-Includes expressing numbers as a product of prime factors, finding the Lowest Common Multiple (LCM) and Highest Common Factor (HCF) of two or more numbers.
– Calculate with and interpret standard form A × 10n, where 1 ≤ A < 10 and n is an integer
1.2- Place value and rounding
• Make estimates of numbers, quantities and lengths, give approximations to specified numbers of significant figures and decimal places and round off answers to reasonable accuracy in
the context of a given problem
e.g. By writing each number correct to one significant figure, estimate the value of ( \(\frac{41.3}{9.79 × 0.765}\))
– Use standard units of mass, length, time, money and other measures (including standard compound measures) using decimal quantities where appropriate
– Estimate answers; check calculations using approximation and estimation, including answers obtained using technology
-Round numbers and measures to an appropriate degree of accuracy (e.g. to a specified number of decimal places or significant figures); use inequality notation to specify simple error intervals due to truncation or rounding
– Apply and interpret limits of accuracy
Approximations
If the side of a square field is given as 90m, correct to the nearest 10m.
The smallest value the actual length could be is 85m (since this is the lowest value which, to the nearest 10m, would be rounded up to 90m). The largest value is 95m.
Using inequalities, 85<length <95.
Sometimes you will be asked the upper and lower bounds of the area. The area will be smallest when the side of the square is 85m. In this case, the area will be 7725m². The largest possible area is 9025m² (when the length of the sides are 95m).
1.3- Adding and subtracting
– Use the four operations for calculations with whole numbers,
decimals and vulgar (and mixed) fractions, including correct ordering
of operations and use of brackets
1.4- Summary and review
– Calculate squares, square roots, cubes and cube roots of numbers
-Includes recall of squares and their corresponding roots from 1 to 15 and cubes and their corresponding roots from 1 to 10.
Types of Numbers
Integers are whole numbers (both positive and negative, including zero). So they are …, -2, -1, 0, 1, 2, …. So a negative integer is a negative whole number, such as -3, -10 or -23. Natural numbers are positive integers.
A rational number is a number which can be written as a fraction where numerator and denominator are integers (where the top and bottom of the fraction are whole numbers). For example \(\frac{1}{2}\),4,1.75 =\(\frac{7}{4}\).
Irrational numbers are numbers which cannot be written as fractions, such as pi and √2. In decimal form these numbers go on forever and the same pattern of digits are not repeated.
Square numbers are numbers which can be obtained by multiplying another number by itself. E.g. 36 is a square number because it is 6 x 6 .
Surds are numbers left written as √n , where n is positive but not a square number. E.g. √2 (see ‘surds’).
Prime numbers are numbers above 1 which cannot be divided by anything (other than 1 and itself) to give an integer. The first 8 prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19.
Real numbers are all the numbers which you will have come across (i.e. all the rational and irrational numbers). All real numbers can be written in decimal form (such as 3.165).
A factor (or divisor) of a number is a number which will divide into your number exactly. So you can divide a number by one of its factors and you won’t be left with a remainder. For example, 3 is a factor of 6 because you can divide 6 by 3 and you won’t be left with a remainder (you get 2).
Prime Factor Decomposition
An important fact is that any number can be written as the product (multiplication) of prime numbers in one way. For example, 20 = 5 x 2 x 2 . This is the only way of writing 20 as the product of prime numbers. Writing a number in this way is called prime factor decomposition.
g 36=6× 6 = 3²×2²
– If ab3=54, Find a and b ?
LCM and HCF
The least (or lowest) common multiple (LCM) of two or more numbers is the smallest number into which they evenly divide. For example, the LCM of 2, 3, 4, 6 and 9 is 36.
The highest common factor (HCF) of two or more numbers is the highest number which will divide into them both. Therefore the HCF of 6 and 9 is 3.
g HCF (6,9)=3 and LCM(6,9)=18
HCF(6,9)×LCM (6,9)=3×18=54= 6×9
1.6- Assessment 1
Question 1 : Write the following numbers as a fraction : 2.13131313….. ; 6.25252525….. ?
Question 2 : Calculate the LCM and HCF of 8 and 12 ?
Question 3 : Here’s a number machine. What is the output when the input is 10?
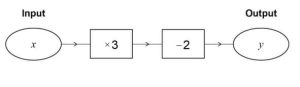
Question 4 : Here’s that number machine again. What is the output if the input changes to -7?