3.1- Introduction
• Calculate unknown angles and give simple explanations using the
following geometrical properties:
(a) angles at a point
(b) angles at a point on a straight line and intersecting straight lines
(c) angles formed within parallel lines
(d) angle properties of triangles and quadrilaterals
(e) angle properties of regular and irregular polygons
(f) angle in a semi-circle
(g) angle between tangent and radius of a circle
(h) angle at the centre of a circle is twice the angle at the circumference
(i) angles in the same segment are equal
(j) angles in opposite segments are supplementary

Angle properties of polygons includes angle sum.

3.2- Angles and lines

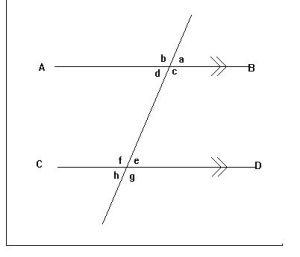
Lines AB and CD are parallel to one another (hence the » on the lines).
a and d are known as vertically opposite angles. Vertically opposite angles are equal. (b and c, e and h, f and g are also vertically opposite).
g and c are corresponding angles. Corresponding angles are equal. (h and d, f and b, e and a are also corresponding).
d and e are alternate angles. Alternate angles are equal. (c and f are also alternate). Alternate angles form a ‘Z’ shape and are sometimes called ‘Z angles’.
a and b are adjacent angles. Adjacent angles add up to 180 degrees. (d and c, c and a, d and b, f and e, e and g, h and g, h and f are also adjacent).
d and f are interior angles. These add up to 180 degrees (e and c are also interior).
Any two angles that add up to 180 degrees are known as supplementary angles.

3.3- Triangles and Quadrilaterals
Using some of the above results, we can prove that the sum of the three angles inside any triangle always add up to 180 degrees.

A quadrilateral is a shape with 4 sides.

For any quadrilateral, we can draw a diagonal line to divide it into two triangles. Each triangle has an angle sum of 180 degrees. Therefore the total angle sum of the quadrilateral is 360 degrees.

3.4- Congruence and Similarity
• Solve problems and give simple explanations involving similarity and
congruence
• Calculate lengths of similar figures
• Use the relationships between areas of similar triangles, with
corresponding results for similar figures, and extension to volumes
and surface areas of similar solids

3.5- Polygon angles
The exterior angles of a shape are the angles you get if you extend the sides.
A polygon is a shape with straight sides. All of the exterior angles of a polygon add up to 360° because if you put them all together they form the angle all the way round a point

3.6- Summary and Review

3.7- Assessment 3
Question 1- Calculate the sum of interior angles of an octogon and a decagon?
Question 2- Which of these shapes has the most sides? Hexagon, Octagon, Triangle, Rhombus.
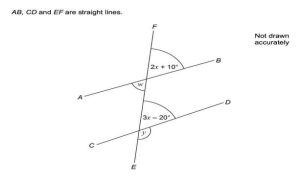
Question 3 – AB, CD and EF are straight lines. We assumes that AB and CD are parallel. What is the angle y?

Question 4 : AB is not parallel to CD. Angle w is 60° , What is angle y?