Discontinuity and Rate of Change

Points where f(x) fails to be continuous are called discontinuities of f(x) and f(x) is said to be discontinuous at these points. In a graph of a continuous function the pencil need never leave the paper, while for a discontinuous function this is not true since there is generally a jump taking place.

Slope of Tangent as Limit

Difference Quotient Applications

Example : f(x) = \({3x^3 -5x +4} \)

\(\frac{f(x+h) - f(x)}{h}\)=\( \frac{3(x+h)^2 - 5(x+h) +4 -(3x^2 - 5x + 4)}{h}\)

=\(\frac{3x^2 + 6xh + 3h^2 - 5x - 5h +4 - 3x^2 + 5x - 4}{h}\)

=\(\frac{6xh + 3h^2 - 5h}{h}\)

=\( 6x+3h -5 \)

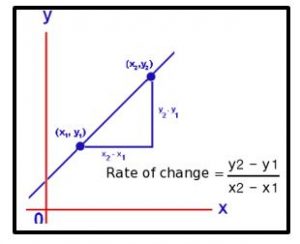
Rates of Change

Limits of Functions

Limit of a composite function

If f(x)  and g(x) are functions such that lim _(x->c)g(x)= L  and   that

lim f(x)_(x->L)= L, then

lim _(x->c)f(g(x)) = f( lim _(x->c)g(x))=f(L)

Continuity

3 conditions :

• lim_(x->x0f(x)=L exists
• f(x) is defined at x₀
• f(x₀)= L

L’Hôpital ‘s rule

L’Hospital’s Rule says that if we have an indeterminate form  \(\frac{0}{0}\) or \(\frac{\infty}{\infty}\)

Then , we must differentiate the numerator and differentiate the denominator and then take the limit.

lim_(x->a)\(\frac{f(x)}{g(x)}\)= lim_(x->a)\(\frac{f'(x)}{g'(x)}\)

Squeeze theorem

If g(x) ≤ f(x) ≤ h(x)  for all x close to a, but not equal to a. If lim_(x->a)g(x)= L  and

lim_(x->a)h(x)= L, then lim_(x->a)f(x)= L

Special limits

lim_(x->0)\(\frac{sinx}{x}\) = 1

 lim_(x->0) \(\frac{cosx -1}{x}\) = 1

 lim_(x->∞) \((1 +\frac{1}{x})^x\) = e

lim_(x->0)\(({1+x})^{\frac{1}{x}}\) = e

 lim_(x->0)\(\frac{e^x - 1}{x}\) = 1

lim_(x->0)\(\frac{x - 1}{ln x}\)