Review Compound Angle Formula

sin(A+B)= sinA cosB + sinB cosA

sin(A-B)= sinA cosB – sinB cosA

sin2A = 2sinAcosA

cos(A+B)=cosA cosB – sinA sinB

cos(A-B)=cosA cosB  + sinA sinB

cos 2A = 2cos²A – 1

cos2A = 1-2sin²A

tan(AB )=    \(\frac{tan A\pm tan B}{1\mp tanA tanB }\)

Review Radian Measurements

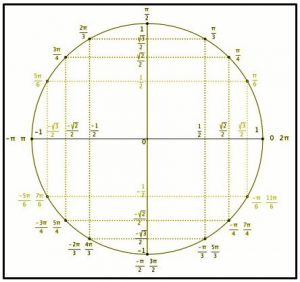
180º =\(\pi\) rad

60º=\(\frac{\pi}{3}\) rad

30º= \(\frac{\pi}{6}\)rad

90º= \(\frac{\pi}{2}\)rad

360º=2\(\pi\) rad

Derivatives of Trigonometric functions

\(\frac{d(Sin~x)}{dx}\)= cos x                     \(\frac{d(csc~x)}{dx}\)  = – csc x cot x

\(\frac{d(cos~x)}{dx}\) = -sin  x                 \(\frac{d(sec~x)}{dx}\)     = sec x  tan x

\(\frac{d(tan~x)}{dx}\)= -sec²x              \(\frac{d(cot~x)}{dx}\) = – csc² x

Further Trigonometric Limits

lim_(x->0)\(\frac{sin x}{x}\)=1 

lim_(x->0)\(\frac{cos x-x}{x}\)=1 

 lim_(x->0)\(\frac{tan x}{x}\)=1 

Derivative of other Trigonometric Functions

cosec x = \(\frac{1}{sin x}\) =>  (cosec x)’= -cotx cosecx

sec x = \(\frac{1}{cos x}\)    =>   (sec x)’= secx tanx

cotan x = \(\frac{1}{tan x}\)  =>    (cotan x)’= cosec²x

Inverse of trigonometric functions

 If y= sin x   then x=arcsin y or x= sin^-1y

If y= cos x   then x=arccos y or x= cos^-1y

If y= tan x   then x=arctan y or x= tan^-1y

Applications of Trigonometric Functions

Trigonometric functions are used in the calculation of integrals by substitution, use the following :

For \(\sqrt{(a^2 -b^2)}\)  apply, x = a sinθ

For \(\sqrt{(a^2 -b^2)}\)  apply, x = a tanθ

For \(\sqrt{(a^2 -b^2)}\)  apply, x = a secθ